Last updated on March 13th, 2024 at 02:37 am

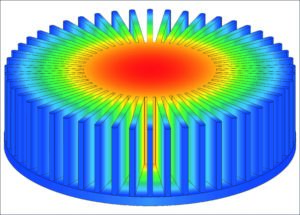
Fins are used to enhance the heat transfer on a surface by increasing the surface area for heat transfer to take place.  For convective heat transfer from a surface, the governing equation is:

Q=h*A*(Ts-Tinf)

Where Q is the rate of heat transfer from a surface to a fluid, h is the convective heat transfer coefficient, A is the area of the contact between the surface and the fluid, Ts is the surface temperature, and Tinf is the fluid temperature.  

While adding a fin to a flat surface increases the surface area exposed to the fluid (A), any fin material lacking infinite thermal conductivity results in a temperature drop down the length of the fin. This decreases Ts over a portion of A.  Also, the presence of the fin may change or disrupt the fluid flow. Which can decrease the convective heat transfer coefficient (h).  In an extreme case, it is even possible for the presence of fins to decrease the heat transfer from a surface.  Thus, it is important to be able to quantitatively evaluate the performance of a proposed fin.

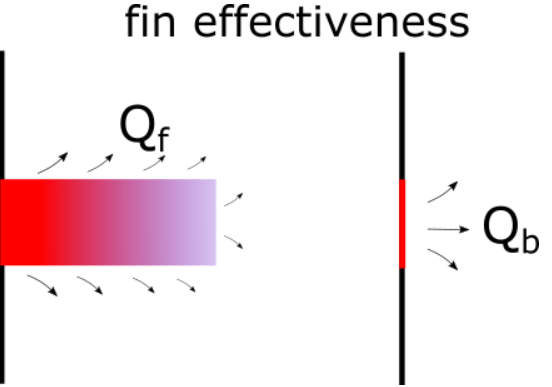
Measures of Fin Performance

There are two common measures for evaluating fin performance.  Fin effectiveness is defined as the ratio of the amount of heat that passes through the fin to the amount that would have been transferred without the fin:

εf = Qf /(h*Ab*(Ts-Tinf))

where Qf is the actual heat transfer through the fin, and Ab is the surface area occupied by the base of the fin.  Of course, it is desirable to make the fin effectiveness as large as possible.  A fin effectiveness greater than 2 is a common rule-of-thumb requirement for adding fins to a surface.

It is useful to consider a concrete example of fin effectiveness.  For the particular case of a fin of constant cross-section, and with the assumption of equal convective heat transfer coefficient for the finned and unfinned cases, and using the result for Qf for an infinite fin length, the fin effectiveness can be expressed:

εf = (k*P/(h*Ab))^0.5

where k is the thermal conductivity of the fin material, and P is the perimeter of the fin circumscribing the fin cross-sectional area (which is Ab, since we are talking about a fin of constant cross-section).

Obviously, in this case, fin effectiveness increases in direct proportion to the thermal conductivity of the fin material.  Cost, manufacturability, durability, and other considerations are important design considerations. But strictly from a thermal performance perspective, the higher the thermal conductivity of the fin, the better. 

Fin Thickness

It is also clear from this equation that a large value for the ratio of P/Ab will increase fin effectiveness.  Thin fins tend to be more desirable than thick fins.  Finally, note that the convective heat transfer coefficient is in the denominator which demonstrates why the addition of fins is most desirable when the heat transfer coefficient is low, and for the gas-side on gas-to-liquid heat exchangers.

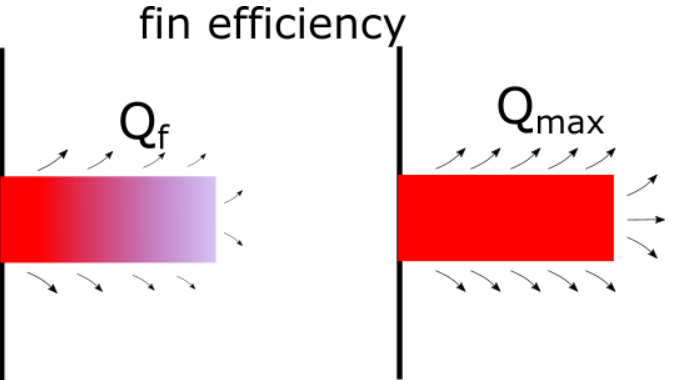
A second measure for evaluating fin performance is fin efficiency.  This is defined as the ratio of the actual heat flow, to the maximum possible heat flow, through the fin.  

ηf=Qf/Qmax

Where Qmax, the maximum possible heat flow, would occur if the entire surface of the fin were at the temperature of the base.  For a straight fin of uniform cross-section, the fin efficiency will be 1 for a fin of zero length (i.e. no fin at all, hence no heat transfer enhancement) and will be 0 for a fin of infinite length (i.e. a fin with the theoretical potential, Qmax, of infinite heat transfer).  Real and useful fins will fall between these extremes of efficiency.

Pragmatically, fin efficiency can be calculated from a heat transfer analysis of a particular fin configuration. And then plotted as a function of fin design parameters.  The resulting plot is usable in the fin design process.

Fin Effectiveness & Fin Efficiency

Fin effectiveness and fin efficiency give two very different, but complementary, ways of looking at fin performance.  For a fin designer, it is important to consider both indicators in assessing the thermal attributes of the fin.  As mentioned earlier, many non-thermal considerations may heavily influence the final design.  These include cost, durability, manufacturability, weight, fouling resistance, fluid compatibility, and many others.

Biography

James Stevens is a professor in the mechanical and aerospace engineering department at the University of Colorado at Colorado Springs.  His background is in numerical and analytical heat transfer analysis. Covering both steady-state and transient situations with applications to thermal history, thermal response, electronic cooling, temperature profiles, thermal design, heat flow rate determination, and more. He also works in applied thermodynamics with applications for renewable energy, HVAC, air engines, novel heat engines, and more. He has over 30 years of experience in higher education teaching undergraduate and graduate classes. Performing research, doing course and curriculum development, and advising students.